Quantum Field Theory on the Edge of Metaphysics - Part III
From Mental to Divine Causation?
In the two previous posts (link, link) I clarified the context in which the interaction problem must be thought to be embedded according to our current understanding of the physical world.
Now, we can see new avenues for conceiving of mental causation. When analyzing principles of mind-matter interaction within a quantum theoretical framework, we cannot abstract from the fact that the concept of physical causality in quantum physics is significantly different from its classical and relativistic counterparts due to its stochastic nature.
From Classical to Quantum Causality
In a Newtonian (or should we say ‘Cartesian’?) universe of classical mechanics, as well as within the realms of special and general relativity, the causal structure is defined by differential equations that determine the dynamical evolution of a system’s physical state. Once the initial and boundary conditions are fixed, the solutions uniquely specify, say, the point-particle's state of motion, its potential and kinetic energy, etc.
These equations can describe highly complex dynamical behaviors, including chaotic ones. For example, the animated GIF illustrates the oscillations of a double pendulum initiated from three slightly different initial conditions. Even the smallest variation in the starting position leads to significantly diverging trajectories over time. This looks very messy, uncertain, almost random. But this is not the kind of uncertainty one finds in QM.
Because, the equations of motion governing these chaotic systems are still unique and, at least in principle, allow for precise predictions of the system's future state, which can be calculated with a computer program to achieve virtually infinite precision. The equations uniquely determine, with certainty, only one possible outcome.
Equations —> One certain outcome
Consequently, the system's evolution over time is pre-determined. The present state will uniquely determine the future state, leaving no room for a ‘freedom to choose otherwise.’ That’s what the classical physical causal determinism is about, leaving no room for free will.
In QM, the situation is considerably more subtle. Essentially, quantum stochasticity reflects the wave-like nature intrinsic to QM and QFT. It underpins quantum superposition states, interference phenomena, and, crucially, the principles of quantum uncertainty that characterize indeterminate quantum states (Heisenberg’s uncertainty principle and the energy-time uncertainty; something we already discussed here.)
Also in QM, like in classical mechanics, the equations are unique and their solutions are determined by the physical context; however, they provide probabilities rather than certainties. For instance, in the famous double-slit experiment, the equations can only predict the probability of finding an electron, which has passed through the slits, at a specific point on the screen, based on an interference pattern. The equations are ‘deterministic,’ only in the sense that they uniquely define a probability function, but they do not guarantee a specific outcome—such as the location of the next electron. Probability conveys likelihood, not certainty.
Equations —> Most probable outcomes
Therefore, when physicists—especially those who lean towards deterministic, reductionist, and classical worldviews—claim that quantum mechanics is a deterministic theory, they aren’t wrong but are deceptive. Because the differential equations that govern the time evolution of a quantum state are 'deterministic' only in a statistical sense; they uniquely specify the wavefunction and, consequently, the probability density function derived from the so-called Born rule. The Schrödinger and Dirac equations are fundamental physical laws that dictate the dynamical evolution of a quantum system over time, in terms of probabilities over a set of possibilities, not a single actuality. While the timing and nature of single events are constrained probabilistically, they are not uniquely predetermined by the past conditions. This means there is still room (limited by statistical variance), which raises the possibility that Nature may 'choose' which events within a state of potentiality will manifest into actuality and when that will happen next.
For example, consider the radioactive decay of the element Bismuth-212. A single Bi-212 atomic nucleus has a lifetime of about an hour, which means that after an hour, there is a 50% chance it has decayed and a 50% chance it has not. However, you will never know exactly when this is going to happen. What you can say is that, for example, there is an approximately 16% chance of decay within the first 15 minutes and a roughly 3% chance that the nucleus is still intact after five hours. Moreover, there are two competing decay modes: a 64% chance of decaying via a β-decay into Polonium-212 and a 36% chance of decaying via α-decay into Thallium-208. What determines which of the possible processes will take place and when?
According to standard quantum theory, the answer is that, apart from the stochastic constraints, there is no other underlying cause or local hidden variable determining the time and kind of decay; it is simply a random occurrence. If we assume quantum theory is a non-local theory without hidden variables,1 we might even argue that there is an inherent non-spatial, and 'acausal' or 'self-causal' kernel within quantum phenomena. Heisenberg’s uncertainty principle, which imposes limits on our ability to determine simultaneously a particle's position and momentum, or the energy-time uncertainty relation, which highlights the energetic indefiniteness of quantum states with finite lifetimes, are not merely epistemic limitations; they are ontological aspects of quantum phenomena. The uncertainty we face is not a result of our limited knowledge; rather, it is an inherent aspect of reality. The timing of the next nuclear decay and the specific state into which the wavefunction will collapse are unpredictable, limited only by the constraints of quantum uncertainty. This is not because we don’t understand the causal principles underlying this uncertainty; rather, it is because of the inherently random nature of quantum phenomena. Physicists often refer to a theory in which stochasticity lacks hidden variables, without delving into the philosophical implications. However, quantum uncertainty is framed in terms of potentiality rather than in terms of a deterministic evolution of actualities. This interpretation might not resonate with the philosophical commitments of physicalists and naturalists due to its teleological nuances, but it lends itself to metaphysical frameworks of mental causation.
Causality Without Interactions
In previous posts, we discussed how the interaction problem of mental causation often stems from outdated notions of causation rooted in classical physics. These ideas no longer align with modern physical understanding. However, we also fail to recognize that the state of a system depends not only on the interactions that determine its evolution but also on the order in which these interactions occur. The diverse and seemingly insurmountable conceptual metaphysical difficulties appearing in the classical physical context can be resolved at once if we recognize that the history of the world is shaped not only by the events that have influenced it but also by the sequence in which these events have unfolded. The order of events is just as causally significant as the events’ dynamical type and magnitude.
A straightforward example of this circumstance is the motion of an object in space resulting from stepwise changes in direction and distance.
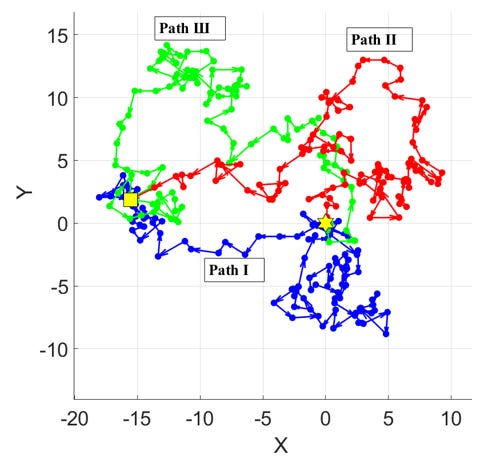
Consider an ordered set of 100 vectors with random orientations and random lengths in a 2D Cartesian coordinate system, as shown in Fig. 4. Each vector indicates a direction and a length to travel.
Randomly select one vector at a time and observe the resulting path. Begin at a point, such as the origin at (0,0), and add each vector sequentially. What kind of journey will this create? If the vectors are randomly oriented and have random lengths, say ranging from 0 to 2.5, you will ultimately trace a random walk. For example the blue random walk—”Path I”—in Fig. 5. It starts at the yellow star in (0,0) and ends at the yellow square.
Now, do this all over again, starting from the yellow star once more. This time, select the same randomly oriented vectors but arrange them in a different order. Sum them up again, and you will arrive at the same yellow square, though this time you will have taken a different route, say the red “Path II.”2 Now, do this a third time: choose the same vectors again, but shuffle their order and follow the new path. You may now traverse the green random “Path III.” And so on…
The key point is that the path is determined not only by the direction and length of the vectors but also by the order in which one selects them. The blue, red, and green random walks comprise all the same vectors but are arranged in three distinct orders. The number of possible paths that can be realized corresponds to the number of permutations of the elements of the vector set, which is proportional to N! (‘N factorial’). For N=100, the number of possible histories is enormous, nearly infinite—that is 1*2*3*4*5…..*99*100. Consequently, the very same events can lead to vastly different histories depending on the order in which they occur.
The decisive aspect is that any permutation of the same vector set does not change the probability with which each vector appears. Because the vector elements remain the same, regardless of their combinatorial arrangement. The probability distribution of the vectors is invariant. This is obvious, as they are always the same vectors. Emphasizing this (only seemingly) trivial point will be crucial next.
Thus, shifting the causal principle of a mental agent, whether spatial or non-spatial, from interactions based on physical forces to a conscious causal power that engages with potentialities—specifically, the temporal ordering of quantum microphenomenal events—constitutes a form of causality that selects and actualizes a history from a set of many possible histories. The actualization of the path, or ‘history’, does not require conventional interactions, defined as a force exchange, to exercise a causal power. Instead, a volition that can permute the sequence of possible events is sufficient for efficient causation. The interaction problem doesn’t arise because this is a causal principle that doesn’t need ‘interactions’ or ‘transference’ of ‘substances’ in the first place. It relies solely on a causal power to permute the time series of actualizations from a specified set of potentialities.
This 'combinatorial causality' does not alter the frequency of outcomes and, therefore, does not affect the probability function determined by the Schrödinger equation. As a result, no laws of physics need to be modified, and there are no issues with conservation principles. The laws of QM inform us about probabilities—that is, the potentialities—but not about when these potentialities must become actualized and with what order. In other words, a mind does not need to interact in the first place, or create energy and generate forces from nothing, thereby violating the conservation of energy principle. It only requires a volition that rearranges the order of events to select one history from the countless possible ones.
From Mental Causation to Divine Causation?
This approach could also be interpreted from a panpsychist perspective, suggesting that all quantum processes in the universe might be fundamentally grounded in proto-mental choices, which I refer to as ‘libertarian quantum panpsychism.’3
Notice how the problem of mental causation could be extended to a broader question that encompasses theological and teleological aspects. From a theistic perspective, if we believe in an almighty creator who orders, regulates, and intervenes in its creation, we must consider how such a transcendent and non-physical being could interact with physical affairs. This presents the same interaction problem, with the atheist raising similar objections: how can a ‘divine causation’ (or divine ‘interaction,’ ‘action,’ ‘intervention,’ or whatever term you prefer) be possible in a universe governed by conventional laws of physics? Is the theist compelled to reject the principle of energy conservation, suggesting that God occasionally interferes with the universe, thus violating this principle? Perhaps divine causation occurs only sporadically or very weakly, preventing us from observing energy fluctuations that arise from nowhere. But what if God's Mind were to intervene continuously? In that scenario, energy would need to be created from nothing on a perpetual basis. Of course, one might argue that God is God, is almighty, and certainly could do so. However, if this continuous miraculous creation of energy from nothing truly occurs, why has no evidence of it been found? If a universal consciousness exists that controls and orders the fate of the universe, influencing everything at every microsecond and at every point—not just during miraculous events—then where is all this new energy?
Perhaps this isn't necessary. There may be a subtler mechanism at play before our eyes, one that possess greater causal power than the lightning of a deity in the clouds and is even more interesting from a metaphysical standpoint than a crude generation of energy from nothing.
I have just demonstrated that this is not only consistent with the laws of quantum physics, but that these laws even suggest the existence of such a mechanism. When Einstein claimed that “God doesn’t play dice,” he overlooked the causal power of dice. God not only plays dice but is, in fact, all the dice, tossing them—that is, Itself—in the right order and at the right time.
The subscription to Letters for a Post-Material Future is free. However, if you find value in my posts and would like to support my work, you can make a small financial contribution by buying me one or more coffees. You can also support me by ordering one of my books or follow one of my online courses. Thank you in advance!
Some might favor interpretations of QM, such as the Many Worlds Interpretation, de Broglie-Bohm mechanics, superdeterminism, or other speculative frameworks with local hidden variables that at least partially recover our everyday classical spatiotemporal realism. I find these interpretations implausible and lacking credibility. The evidence suggests that we should embrace the message of Nature rather than cling to anthropomorphic views of reality. I will align with those interpretations that endorse a non-local, ontological indeterministic realism without hidden variables.
It should not be surprising that the combination of randomly oriented vectors with varying lengths starting from the same point always end up at the same endpoint, regardless of the order in which they are added. This is due to the commutative property of vector addition: The sum of all vectors remains constant. Consequently, the final position of the random walk is unaffected by the order in which the vectors are arranged.







"When Einstein claimed that “God doesn’t play dice,” he overlooked the causal power of dice. God not only plays dice but is, in fact, all the dice, tossing them—that is, Itself—in the right order and at the right time."
This certainly gives a whole new spin on Leibniz's "the best of all possible worlds".
Isn’t the assumption ‘mind is a non-physical substance’ itself problematic? Mind-substance should be amenable to mathematical representation to study its interaction with matter. It appears inconceivable how mind, with its ineffable beliefs, desires and intentions, could be captured in a mathematical formulation. There is no such difficulty with other ‘non-physical’ entities such as electromagnetic fields.